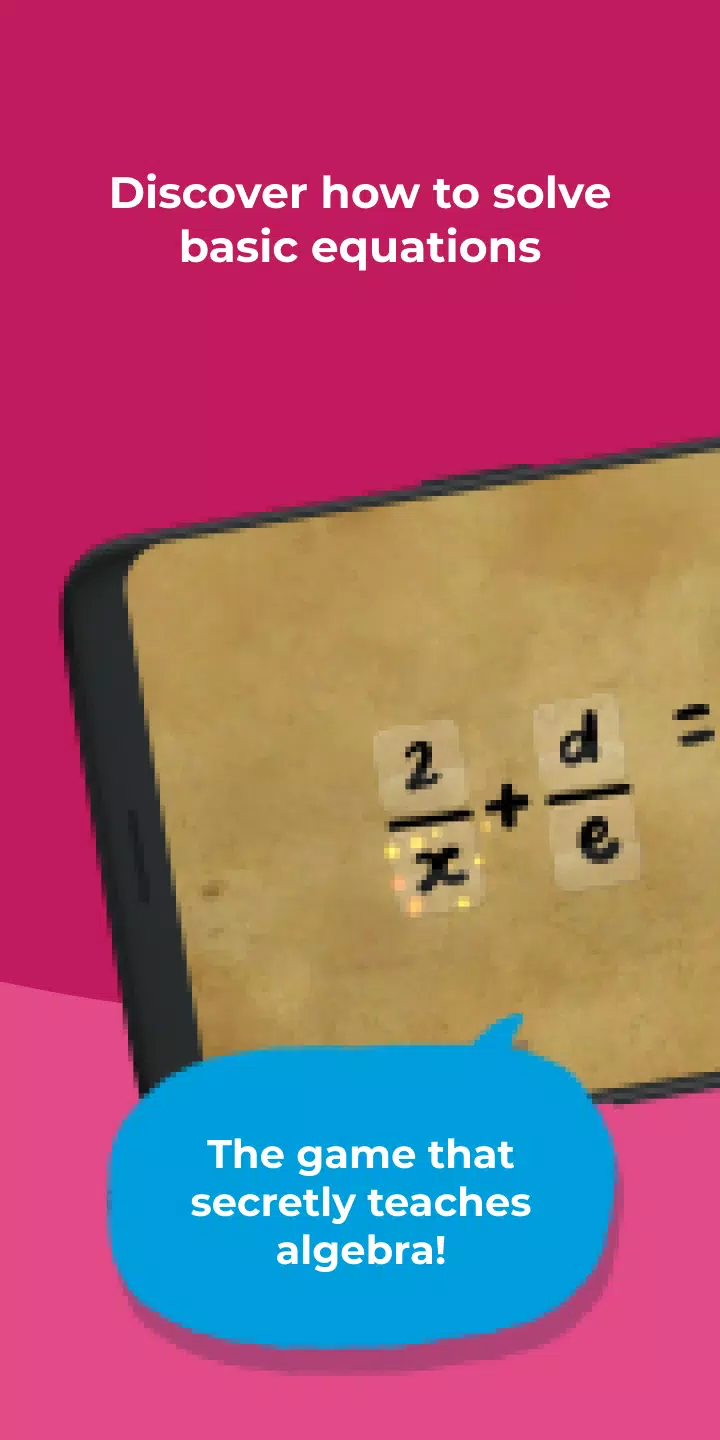| App-Name | Kahoot! Algebra by DragonBox |
| Entwickler | kahoot! |
| Kategorie | Lehrreich |
| Größe | 95.2 MB |
| Letzte Version | 1.10.7 |
| Verfügbar auf |
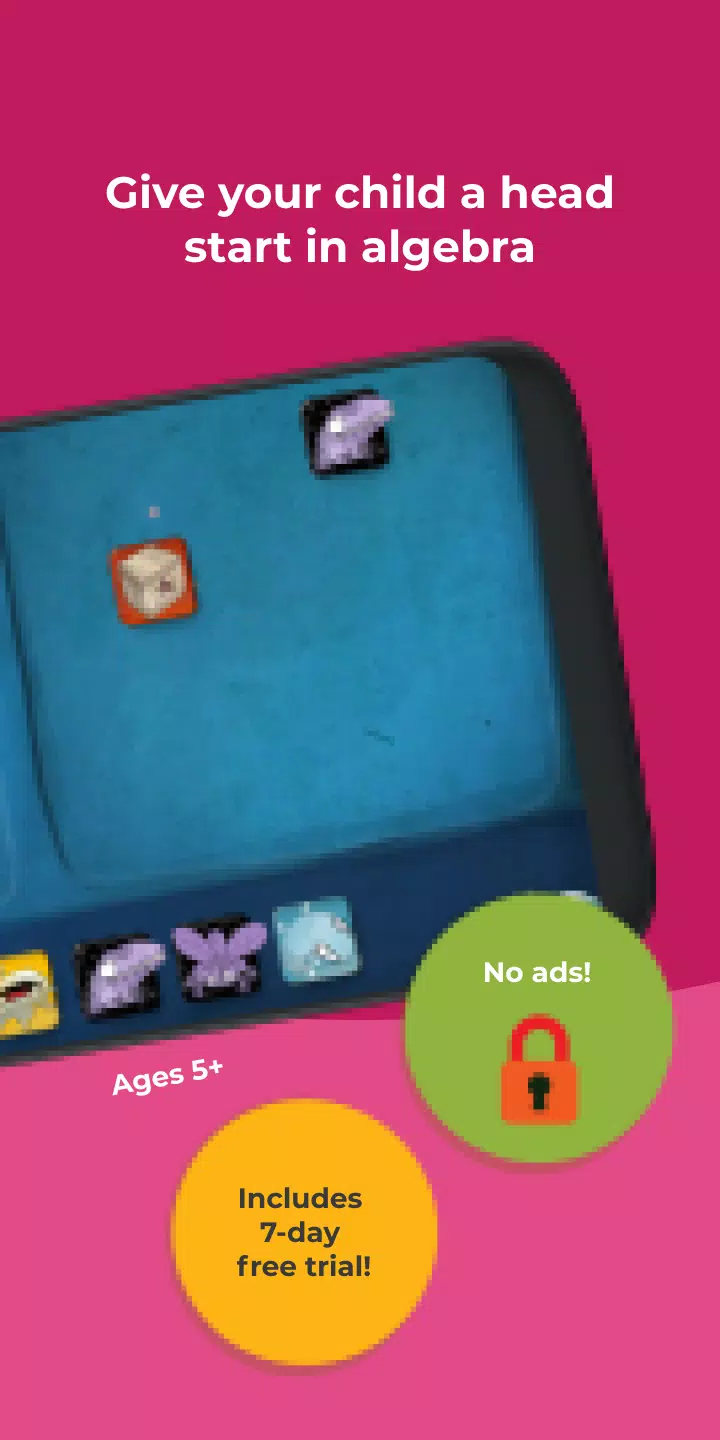
Das Erlernen der Lösung von Gleichungen kann eine ansprechende und lohnende Erfahrung sein, insbesondere mit Tools wie Kahoot! Algebra von Dragonbox. Diese App, die in einem Kahoot!+ -Familie -Abonnement enthalten ist, soll junge Lernende in einer unterhaltsamen und intuitiven Weise in die Welt der Algebra einführen.
Abonnementdetails
Zugang zu Kahoot! Algebra by Dragonbox benötigt ein Kahoot!+ Familienabonnement. Dieses Abonnement verfügt über eine 7-tägige kostenlose Testversion, die jederzeit vor Ende der Testversion abgesagt werden kann. Das Abonnement bietet nicht nur Zugriff auf diese App, sondern auch auf andere Premium -Kahoots! Funktionen und mehrere preisgekrönte Lern-Apps, die sich auf Mathematik und Lesen konzentrieren.
Wie das Spiel funktioniert
Kahoot! Algebra von Dragonbox lehrt wichtige algebraische Konzepte wie Addition, Teilung und Multiplikation. Das Spiel verwendet einen einzigartigen pädagogischen Ansatz, der Entdeckung und Experimente betont. Die Spieler beschäftigen sich mit einer farbenfrohen und spielerischen Umgebung, in der sie Karten manipulieren, um die Dragonbox auf einer Seite des Spielbretts zu isolieren. Dieser Prozess führt sie nach und nach in die Operationen ein, die zur Isolierung der Variablen 'x' auf einer Seite einer Gleichung erforderlich sind. Während des Fortschritts wechseln die Karten in Zahlen und Variablen und zeigen die zugrunde liegenden mathematischen Operationen.
Das Spiel ist selbst geführt, aber Eltern können dabei helfen, die im Spiel erlernten Fähigkeiten zur Lösung von Gleichungen auf Papier zu übersetzen. Es ist ein hervorragendes Werkzeug für das Lernen in der Familie und hilft sowohl Kindern als auch Eltern dabei, ihre mathematischen Fähigkeiten zu erfrischen.
Entwicklung und Anerkennung
Dragonbox wurde vom ehemaligen Mathematiklehrer Jean-Baptiste Huynh entwickelt und wurde für seinen innovativen Ansatz zum spielbasierten Lernen gelobt. Es war im Mittelpunkt der umfassenden Forschung des Zentrums für Spielwissenschaft der Universität von Washington.
Merkmale
- 10 progressive Kapitel, unterteilt in 5 Lern- und 5 Trainingsabschnitte
- 200 Rätsel zu lösen
- Deckt die Lösung von Gleichungen mit Zugabe, Subtraktion, Teilung und Multiplikation ab
- Einzigartige Grafiken und Musik, die auf jedes Kapitel zugeschnitten sind
Auszeichnungen
Kahoot! Algebra von Dragonbox hat zahlreiche Auszeichnungen erhalten, darunter:
- Goldmedaille bei den International Serious Play Awards 2012
- Bestes Bildungsspiel beim 2012 Fun and Serious Games Festival
- Bestes ernstes Handyspiel bei The 2012 Serious Games Showcase & Challenge
- App des Jahres und Kinder -App des Jahres bei Gultasten 2012
- Bestes ernstes Spiel bei den 9. International Mobile Gaming Awards (IMGA 2012)
- 2013 On for Learning Award von Common Sense Media
- Bester Nordic Innovation Award 2013 bei den Nordic Game Awards
- Auswahl der Redakteure Auswahl aus der Kinder Technology Review
Medienpraxis
Die App wurde von verschiedenen Medien gelobt:
- Geekdad von Wired: "Dragonbox lässt mich alle Zeiten überdenken, in denen ich eine Bildungs -App 'Innovative' bezeichnet habe.
- Jordan Shapiro von Forbes: "Treten Sie Sudoku beiseite, Algebra ist das ursprüngliche Puzzlespiel."
- Jinny Gudmundsen aus USA Today: "Brillant, Kinder wissen nicht einmal, dass sie Mathe machen."
Neueste Updates
Die neueste Version 1.10.7, die am 20. Oktober 2024 aktualisiert wurde, enthält:
- Eine neue Einstellung der Sprachauswahl, mit der Benutzer ihre bevorzugte Sprache auswählen können, die als Standardeinstellung gespeichert wird, wenn sie von der Gerätesprache unterscheidet.
- Ein neuer Lernweg für bestehende Kahoot! Kinderabonnenten, um das volle Lernpotential ihres Kindes freizuschalten.
Privatsphäre und Begriffe
Weitere Informationen zu Privatsphäre und Bedingungen finden Sie unter:
- Datenschutzrichtlinie: https://kahoot.com/privacy
- Allgemeine Geschäftsbedingungen: https://kahoot.com/terms
-
 Trainer-Pokémon werden 2025 im Pokémon-Sammelkartenspiel wieder auftauchen
Trainer-Pokémon werden 2025 im Pokémon-Sammelkartenspiel wieder auftauchen
-
 Clash of Clans Enthüllt Town Hall 17: Bahnbrechendes Update veröffentlicht
Clash of Clans Enthüllt Town Hall 17: Bahnbrechendes Update veröffentlicht
-
 Stalker 2: Liste aller Artefakte und wie man sie bekommt
Stalker 2: Liste aller Artefakte und wie man sie bekommt
-
 Mastering -Parry -Techniken in bekennender: Ein Leitfaden
Mastering -Parry -Techniken in bekennender: Ein Leitfaden
-
 Shadow of the Depth: Offene Beta jetzt für Android verfügbar
Shadow of the Depth: Offene Beta jetzt für Android verfügbar
-
 Eilmeldung: Ubisoft enthüllt verdecktes NFT-Gaming-Unternehmen
Eilmeldung: Ubisoft enthüllt verdecktes NFT-Gaming-Unternehmen